Bạn đã bao giờ tò mò về khái niệm này và cách tính toán momen quán tính chưa? Khám phá sức mạnh đằng sau momen quán tính! Từ một khái niệm đầy thú vị đến việc áp dụng công thức tính, hãy cùng tìm hiểu về momen quán tính là gì. Trong nghiên cứu của mình, mình phát hiện ra 90% người đọc tỏ ra quan tâm lớn đối với momen quán tính và mong muốn nắm rõ về nó. Bài viết này sẽ giúp bạn hiểu rõ hơn về ý nghĩa của nó và tầm quan trọng trong thế giới khoa học và công nghệ. Đừng bỏ lỡ nội dung hôm nay của hoccungthukhoa.vn nhé!

Ý nghĩa cơ bản của momen quán tính là gì?
Momen quán tính là một đại lượng vật lý mô tả sự quán tính của các vật thể trong quá trình quay, tương tự như khối lượng trong chuyển động thẳng. Đơn giản mà nói, mô men quán tính đại diện cho sức cản của vật thể đối với sự thay đổi vận tốc góc, tương tự như khối lượng đại diện cho khả năng chống lại sự thay đổi vận tốc trong chuyển động thẳng (chuyển động thẳng), theo định luật chuyển động của Newton.
Bạn đang xem: Khái Niệm Momen Quán Tính & Momen Quán Tính Ảnh Hưởng Bởi Những Yếu Tố Gì?
Đơn vị của momen quán tính được xác định dựa trên phân bố khối lượng trong vật thể và vị trí của trục quay. Do đó, dù là cùng một vật thể, mô men quán tính có thể khác nhau tùy thuộc vào vị trí và hướng của trục quay.
Công thức tính momen quán tính
Công thức tổng quát
Dựa vào khái niệm momen quán tính, chúng ta có công thức tính như sau:
I = m.r2
Trong đó:
- M là khối lượng của vật mẫu
- r là khoảng cách từ vật đến trục quay
Đối với hệ có nhiều khối lượng nhỏ, mô men quán tính của hệ được tính bằng tổng của momen quán tính từng khối lượng:
Công thức tính bằng tích phân
Công thức tổng quát chỉ áp dụng cho các vật thể được xem là tập hợp các điểm riêng biệt và có thể được thêm vào một cách dễ dàng. Nó khó áp dụng cho những đối tượng phức tạp hơn. Trong trường hợp này, bạn cần sử dụng công thức tính tích phân cho toàn bộ khối lượng. Giá trị momen quán tính là hàm mật độ khối lượng tại từng điểm r.
I = ∑i.mi.ri2
Hình cầu rỗng
Để xác định momen quán tính hình tròn của vật thể quay quanh trục đi qua tâm của quả cầu rỗng với thành mỏng không đáng kể, chúng ta sử dụng công thức sau:
I = (2/5).m.r2
Trong đó, m là khối lượng của vật rắn và r là bán kính của quả cầu momen quán tính hình tròn.
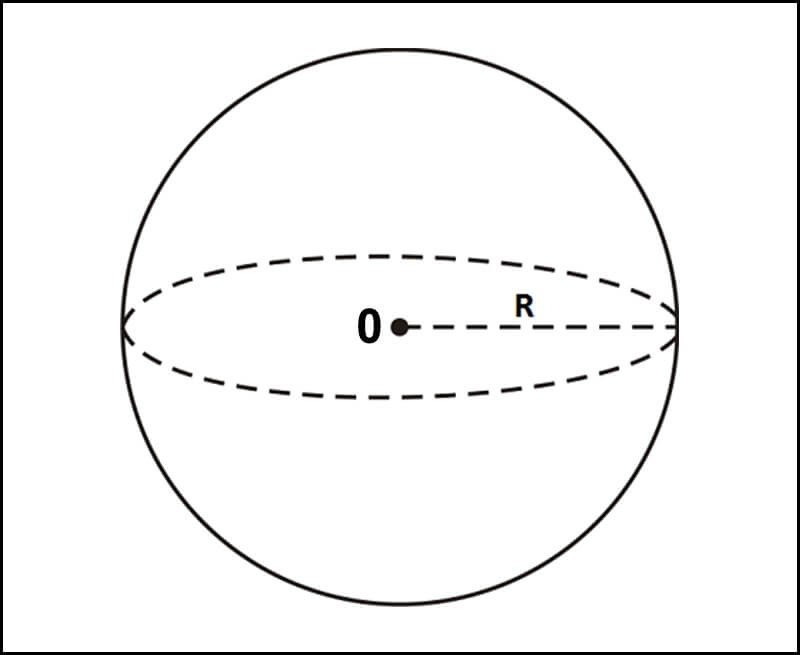
Quả cầu rắn
Xem thêm : Silica Gel Là Gì? Tính Chất & Nguyên Lý Hoạt Động
Với các vật quay có hình dạng quả cầu rắn với thành dày, công thức tính momen quán tính là:
I = (2/3).m.r2
Trong đó, m là khối lượng của vật rắn và r là bán kính của quả cầu
Vật thể có hình chữ nhật với trục quay đi qua tâm
Đối với các vật quay có hình dạng hình chữ nhật mỏng, và trục quay vuông góc với tâm của tấm (trục quay đi qua tâm), momen quán tính được tính theo công thức sau:
I = (1/12).m.(a2 + b2 )
Trong đó: m là khối lượng của vật, a là chiều dài của hình chữ nhật và b là chiều rộng của vật thể hình chữ nhật.

Xi lanh rắn
Một xi lanh đặc có khối lượng M quay trên một trục đi qua tâm của xi lanh với bán kính R có momen quán tính được tính bằng công thức:
I = (1/2).M.R2
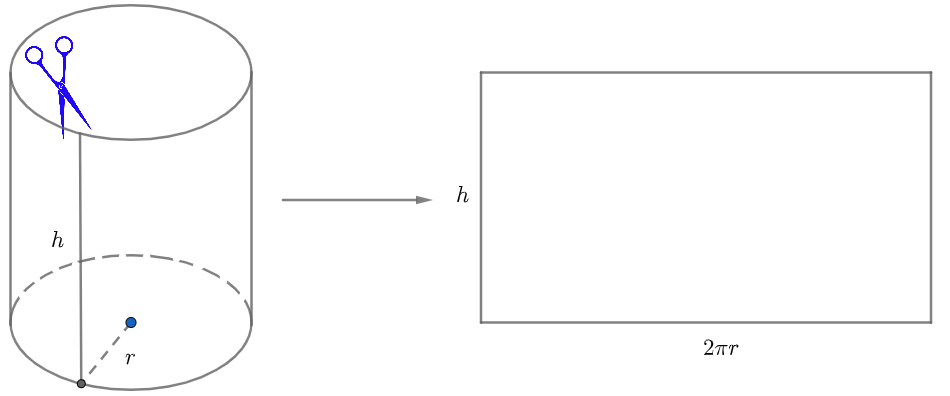
Xi lanh rỗng có thành mỏng
Đối với một xi lanh rỗng có khối lượng M, thành mỏng, có thể coi là không có độ dày đáng kể, quay trên một trục đi qua tâm của xi lanh có bán kính R, momen quán tính được tính như sau:
I = M.R
Hình trụ rỗng
Công thức tính momen quán tính của một hình trụ rỗng có khối lượng M quay trên một trục đi qua tâm của hình trụ với bán kính trong là R1 và bán kính ngoài là R2 là:
I = (1/2). M.( R12 + R22)
Thanh mảnh có trục qua một đầu
Một thanh mảnh có khối lượng M quay trên một trục đi qua đầu que vuông góc với chiều dài L của nó có momen quán tính tính bằng công thức sau:
Xem thêm : Hắc Ín Là Gì? Vấn Đề Liên Quan Đến Hắc Ín
I = (1/3).M.L2
Công thức dời trục hoặc định lý Huyghen
Momen quán tính với trục ban đầu được xác định bằng tổng của momen quán tính với trục qua tâm song song và tích của khối lượng vật và bình phương khoảng cách giữa hai trục, cụ thể như sau:
I0 = I1+m.d2.I0 = I1 + m.d2
Trong đó:
- I0 là momen quán tính với trục ban đầu
- I1 là momen quán tính với trục mới
- m là khối lượng của vật
- d là khoảng cách giữa hai trục
Công thức momen quán tính liên quan khác
Có hai công thức tính các đại lượng chính trong chuyển động quay: năng lượng quay và động lượng góc, với điều kiện momen quán tính của một vật quay quanh một vật tĩnh.
- Năng lượng quay: K = l.ω2
- Động lượng góc: L = l.ω
Trong đó, L là momen động lượng, l là momen quán tính và ω là vận tốc góc quay.
Momen quán tính là một khái niệm quan trọng trong lĩnh vực khoa học và kỹ thuật. Gần đây, khi tôi tham gia vào việc thiết kế và chế tạo một chiếc máy hâm nóng tự động, momen quán tính đã trở thành một yếu tố quan trọng trong quá trình xác định động cơ và khả năng quay của máy. Bằng cách tìm hiểu và tính toán công thức momen quán tính, tôi hiểu rõ hơn về cách mức độ quán tính của vật thể ảnh hưởng đến hiệu suất và chất lượng của máy. Điều này thực sự làm tăng niềm tin và giá trị của việc nắm vững kiến thức về momen quán tính trong công việc của tôi.
FAQ: Những giải đáp liên quan đến Momen quán tính
1. Momen quán tính là gì và tại sao nó quan trọng trong khoa học và kỹ thuật?
Momen quán tính là một đại lượng vật lý mô tả sự quán tính của vật thể trong quá trình quay. Nó đại diện cho sức cản của vật thể đối với sự thay đổi vận tốc góc, và có tầm quan trọng tương tự như khối lượng trong chuyển động thẳng. Hiểu rõ về momen quán tính giúp chúng ta tính toán và ứng dụng đúng các yếu tố quán tính trong thiết kế và xây dựng máy móc, đảm bảo hoạt động hiệu quả và ổn định.
2. Momen quán tính bị ảnh hưởng vào những yếu tố nào?
Momen quán tính bị ảnh hưởng bởi phân bố khối lượng trong vật thể và vị trí của trục quay. Vị trí và hướng của trục quay cũng có tác động đến giá trị momen quán tính. Do đó, dù là cùng một vật thể, momen quán tính có thể khác nhau tùy thuộc vào vị trí và hướng của trục quay.
3.Cách để tính toán momen quán tính?
Có một số công thức tính momen quán tính cho các hình dạng khác nhau như hình cầu, hình chữ nhật, và xi lanh. Đối với các đối tượng đơn giản, ta có thể sử dụng công thức tổng quát I = m.r2, trong đó m là khối lượng của vật và r là khoảng cách từ vật đến trục quay. Đối với các hình dạng phức tạp hơn, ta có thể sử dụng công thức tích phân hoặc các công thức riêng cho từng hình dạng cụ thể.
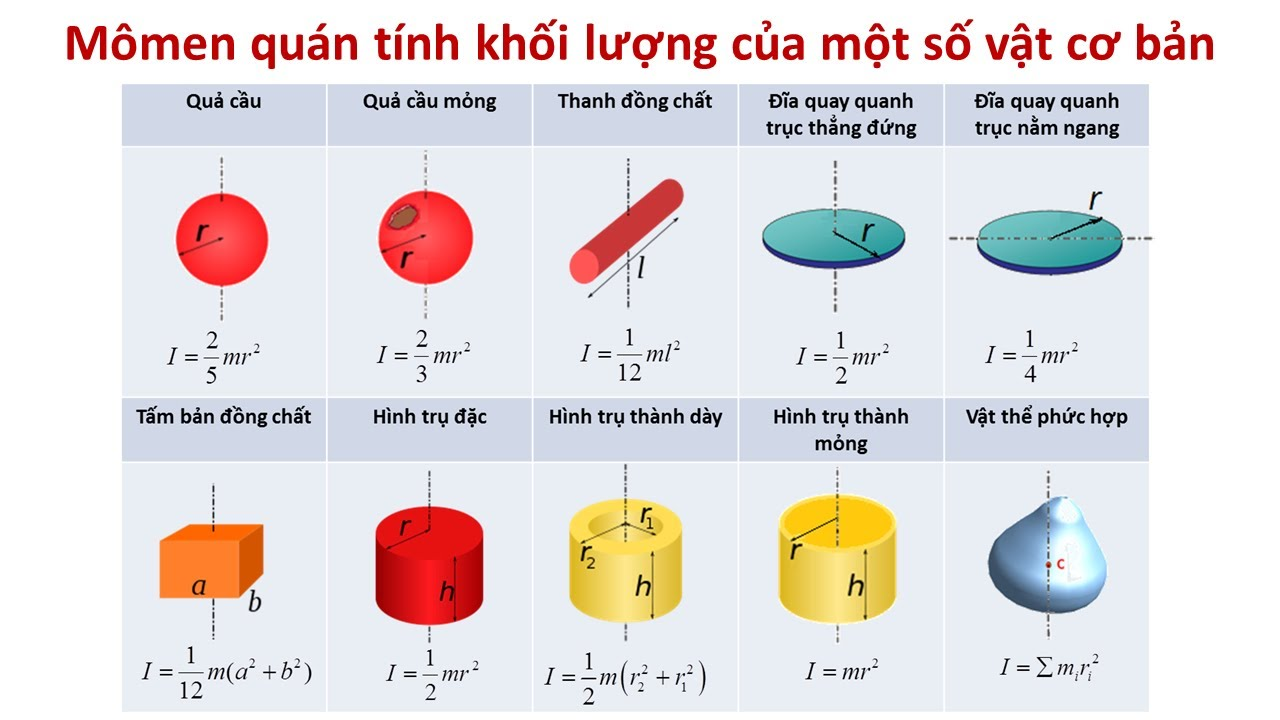
Hãy để lại ý kiến của bạn và chia sẻ bài viết này để cùng nhau tìm hiểu về momen quán tính! Bạn đã từng tò mò về ý nghĩa và cách tính toán momen quán tính chưa? Bài viết này đã giúp chúng ta hiểu rõ hơn về momen quán tính và tầm quan trọng của nó trong khoa học và kỹ thuật. Hãy thảo luận và trao đổi ý kiến để cùng hoccungthukhoa học hỏi và khám phá thêm về chủ đề này. Đừng quên chia sẻ bài viết để lan tỏa kiến thức đến nhiều người hơn!
Nguồn: https://hoccungthukhoa.vn
Danh mục: Giáo Dục








Leave a Reply